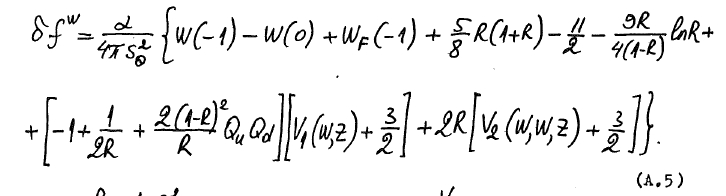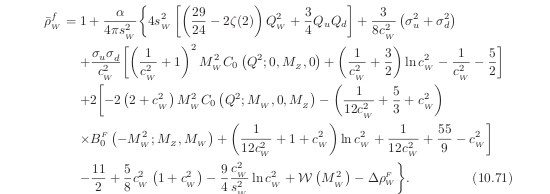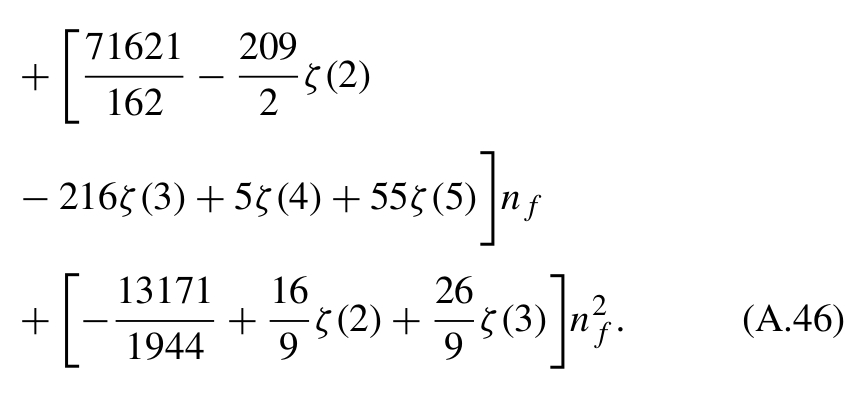ZFITTER code `integration' in Gfitter software - a Documentation of basic facts -

Webpage under construction

This is a private webpage, based on publicly available information. Responsible for the content is the webmaster. Corrections are welcome.

See also the return address
http://zfitter.com
and

zfitter-code-in-gfitter.html - Samples of the `integration' of ZFITTER software in Gfitter/GSM software.
gfitter-gsm-patches.html - Patches of misprints arising from the `integrations'.
gfitter-publications.html - Informations on publications of Gfitter where the use of [next word was misprinted until 24 Oct 2011] ZFITTER software is not quoted.
zfitter-text-in-gfitter-publications.html - Samples of [latex source] text, found in the main Gfitter publication and also in a diploma thesis, taken from latex source files written by ZFITTER authors.

and a documentation of Gfitter publications gfitter-publications.html
and
http://www.cern.ch/Gfitter, official Gfitter webpage
http://gfitter.desy.de, kind of mirror at DESY
The webpage at DESY contains a bit bizarre contents under `Download, gsm'.
A legalized Gfitter/GSM sub-package does not exist; the authors of the potential package were agreed upon to be 14 of the ZFITTER authors and 4 of the Gfitter authors [and not what is written there], and the future licence cannot be the GPL license because of contradiction to the CPC licence of ZFITTER; etc.
[made public at DESY webpages since 21 July 2011, later also at CERN webpages, last check of contents: 04 Aug 2011].

The release of http://gfitter.desy.de/download/ with its misleading informations on Gfitter/GSM triggered the creation and release of this webpage.

Foto: Copyright (2011) tordriemann@googlemail.com
The webmaster: "Wo ZFITTER drin ist, soll auch ZFITTER draufstehen!"

Wo ZFITTER drin ist, soll auch ZFITTER draufstehen

google translator:
Where there is ZFITTER, should also stand upon ZFITTER

ZFITTER
During years from 1985 [or so], the ZFITTER software changed somehow, it consists of about 20000 lines, and no description or pool of publications gives a strict replica of it - we delivered to the community more than 350 pages of description over the years.
This is the general problem faced here. It is nearly impossible to simply re-type from the publications what is coded in ZFITTER, including about 8000 lines of DIZET, the library of Standard Model loop corrections.

There are four ways out for scientists to go:

Invite the authors of ZFITTER to join your new project.
- This was not intended by Gfitter.
Link the existing code [and do not hide this].
[What usually all the many other users of ZFITTER do.]
- This was not intended by Gfitter.
Write your own, better code.
- This was not possible to Gfitter.
Let it go. Give up.
- Gfitter: No.

Gfitter took another way.

03 March 2011

Two of the ZFITTER authors find by a naive, legal google search a repository of the ATLAS collaboration, experimenting at the LHC at CERN,
http://atlas- sw.cern.ch/cgi -bin/viewcvs-atlas.cgi/groups/catsusy/Gfitter/.
The archive is dated approximately in 2008, and the c++ Gfitter software found there is dated approximately in 2006.
It was immediately evident to us, even though we are not familiar with c++, that substantial parts of the subdirectory ./Gfitter/gsm, the Standard Model library of Gfitter, have been 'integrated' from the Fortran software ZFITTER version 6.42 [The first example given below was the first evidence we observed.]

The ./Gfitter/gsm package found by google is here.
The deposit is erased in the meantime. So, we take the freedom to reproduce the package here. As explained in more detail at another place, we consider ourselves as co-authors of the package due to the extensive integration of our software in that package. Further, the licence of the package [see inside] allows this explicitely. Finally, it is impossible to make any use of the sub-package other than some pedagogical demonstrations on copyright etc.

We would like to reproduce also the 'production' version of Gfitter/GSM as it was kindly made available to us on the same day yet (3 March 2011) by Dr. J. Haller, then professor of physics at University Goettingen. Unfortunately, the code was considered by the authors to be proprietary and is so until now. Latest hint on that was given on 11 Sept 2011 again by one of the authors:

"Dieser Code wurde nicht fuer die Oeffentlichkeit gemacht, und das haben Sie zu respektieren."

google tranlator [improved]: "This code has not been done for the public, and you have to respect that."
We are a bit stuck that people come and make out of our open-source code some proprietary one, without asking us.
One may say a lot more on this, but let us stay silent.
We truly want to respect the private sphere of others as much as demanded by them, if possible, and so we follow the demand.

Why do you find this webpage in the internet?
Since more than 5 months, ZFITTER copyright holders try to find a smooth, consensual solution of the situation, created by the "hidden copy-paste-change" of ZFITTER by Gfitter and then "publish" by Gfitter.
We have to state that a dialog on ethics, legality, copyright, intellectual property, Urheberrecht and all that did not evolve. In contrary, there were even times that Gfitter and/or their supporters denied the existence of any serious problem and tried to make the impression that ZFITTER representatives try to "hinder the Cooperation of CERN and DESY" and/or to "hinder the Scientific Progress" [to add on: maybe one should also be concerned avout the "Universal World Peace" or the "Friendship Of GDR And Soviet Union" etc.etc.].

Some of the supporters speak of the "Case Riemann" [in German: "Fall Riemann"].
But it is no case, and it might come out in future that it is truly a "Case Gfitter" [in German: "Fall Gfitter"].
T. Riemann is the spokesperson of ZFITTER and just does what a spokesman has to do.

As far as we know from the exchange of documents and from the seldom direct contact, Gfitter prefers a reflection of the factual status which is quite different from what we consider to be evident.
Supporters of Gfitter are not ready to take notice of ZFITTER's view of the case until now [end of October 2011].

The community:
It was, for a certain term, not appropriate to spread information on the hidden `integrations' in order not to hinder a consensual solution.
Nevertheless, one or the other collegue followed the developments with interest.
About (50 +/- 20)% of the physicists, including those with educational and research responsibilty, spelled out that they do the same as Gfitter [experimentalists in huge collaborations: % even higher] or at least find nothing strange by hidden unauthorized copy-paste-change. Although, being asked for an example by their own, they usually remembered none.
The majority of physicists who also write code to be used by others [not as part of collaborative work, of course] found Gfitter's use of ZFITTER not appropriate.
In contrast, a fraction of responsible scientists assume that open-source software usually is given up by the authors, and thus a hidden `integration' into the work of others then is just to be expected and can be understood as being socially accepted.
The actions by representatives of ZFITTER to get credit for their software were undertaken in German language. From time to time the reactions on this contained a grain of polemics: ".. Attitüde ... setzen von Deadlines .. Stil von Abmahnern .. in krasser Missachtung .. ungeheuerlicher Vorgang .. Eskalationen durch Herrn .. unertraegliche .. Nachstellungen .. unakzeptable Ton .. Toleranz aller Beteiligten nicht .. ueberfordern .. unsaeglich .. unertraeglich .." etc.
Normal citizens:
They often have quite naive opinions: "If they did not ask, it is stolen." Normal citizens, by the way, know quite well from their intensive internet use that open-source-status is not equal to lack-of-legal-conditions-status, even if no explicit legal information is given. This is common knowledge among European people with some education.

Finally,the release of http://gfitter.desy.de/download/ with non-authorized statements on the status of the package Gfitter/GSM and non-authorized files [see e.g. package gsm_23aug2011.tgz there] triggered the creation and release of this webpage.

We have a deep believe in the health of Elementary Particle Physics in Europe, and we believe that the responsibles support our policy of

Zero Tolerance to Plagiarism -- Null Toleranz fuer Plagiate

Not interested in any ethics, legality, politics, polemics or social aspects?
Look at Collins English Dictionary: "Plagiarism is the practice of using or copying someone else's idea or work and pretending that you thought of it or created it."
Or consult a typical Geschaeftsordnung/Betriebsordnung of a typical German research institute: ".. wissenschaftliches Fehlverhalten ..: .. - Verletzung geistigen Eigentums durch - unbefugte Verwertung unter Anmassung der Autorenschaft (Plagiat) ..".
Or, maybe less serious, but quite informal, try de.wikipedia.org/wiki/Plagiat or en.wikipedia.org/wiki/Plagiarism.
Other informative webpages are collected here, linking e.g. to the German Urheberrechtsgesetz.

If this believe in the health of Elementary Particle Physics in Europe is well-founded, then it is truly helpful to have an unbiased look on doubtful cases.
Just in order to clarify them and - if there is nothing unusual, to find this out.
At the other hand, if there is something unusual, we - the particle physics community in Europe - should have an interest to repair bad developments.

But let us come back to the Gfitter data.
Since 12 May 2011 we know who are the authors of Gfitter/gsm:
- Martin Goebel (then diploma student at U. Hamburg, now Ph.D. student at U. Hamburg and DESY-Hamburg, Germany),
- Dr. Johannes Haller (then Junior-Professor of Experimental Physics at U. Hamburg and advisor of Mr. M. Goebel, later Professor of Experimental Physics at U. Goettingen and doctorand's advisor of M. Goebel, and now, starting from 1 July 2011, again Professor of Experimental Physics at U. Hamburg, Germany),
- Dr. Andreas Hoecker (Staff at CERN, Switzerland),
- Dr. Klaus Moenig (Leading Scientist at DESY, Zeuthen site, Germany).

The word 'integrated' has to be interpreted in its classical meaning:
- copy, paste and change
- sell the result as genuin creation of the copying staff [hide the `integration']
Many of the variable names used in ZFITTER have been changed during this 'integration' to Gfitter, so software-based automatized checks would fail; one has to search for identical structures of identities and functions in both codes in order to identify 'derivations'.

The holder of intellectual property [copyright] (Urheberrechteinhaber) on ZFITTER are the authors of the package since about 1985.
There might be supporters of Gfitter who try to disprove this, but we have a strong confidence to hold the copyright.
In addition, the ZFITTER code is software licenced twice by the journal "Computer Physics Communications", where it has been submitted by written permission of the employer of the submitter (TR); see here.
ZFITTER never was informed on `integration' of code into Gfitter or even gave permission to do so.

During weeks following 03 March 2011, two of the ZFITTER authors identify about 175 items of 'integration' of code from ZFITTER into Gfitter. An independent study of another ZFITTER author identifies at least 500 lines of Fortran to be 'integrated'. Both studies do not claim to be exhaustive and do not include `integration' of code from third parties.
Because the source code is handled as being proprietary by the Gfitter group, the software `integrations' have been nearly perfectly hidden.
This webpage reproduces examples of the findings.

During months following 03 March 2011, scanning all the more than 35 Gfitter publications until March 2011, we cannot find any hint in the publications to the fact that software 'integrations' have been performed.
The webpage gfitter-publications.html reproduces the findings.

Since 08 March 2011, ZFITTER authors have been spelling out several expectations against Gfitter:

Gfitter should accept that the `integration' of ZFITTER software would need an explicit agreement by ZFITTER, potentially bound to conditions of use
[due to the ZFITTER copyright held by the ZFITTER authors]
- these conditions of use have been formulated on several occasions, again after 11 May 2011, but have not been fulfilled so far
Gfitter should agree on the fact that there is a substantial amount of software from ZFITTER `integrated' into Gfitter
[a factual statement]
Once software from ZFITTER has been integrated into Gfitter, every Gfitter publication should quote the 2 CPC ZFITTER articles for the use of the ZFITTER software
[due to the CPC licence of ZFITTER held by the ZFITTER authors]
An open-source release of Gfitter would need even a written permission by ZFITTER
[due to the CPC licence of ZFITTER held by the ZFITTER authors]
In the present situation, since 2007 until now, Gfitter has no legal rights to use the software sub-package Gfitter/GSM for numerical calculations or to submit any kind of publications using this package or to make it an open-source package.
We agreed on single-case allowances, to be decided if we are asked for this.
There was one case so far: arXive:1107.0975 [hep-ph]. Any other publication of this kind is not legal; there are more than 35, including some additional ones after 08 March 2011 [the day we spell out the problems around Gfitter].

In October 2011 we documented additionally that in two publications, namely a diploma thesis (2008) and the main Gfitter publication in EPJC60 (2009), there was text from ZFITTER authors hiddenly copied-changed-pasted.

A documentation of the publications of Gfitter from 2007 to 2011 may be found here.

At the present webpage, we document few of the approximately 175 ZFITTER Fortran code pieces [we count each equation with the = sign as a single item] `integrated' into the c++ package Gfitter.

List of ZFITTER Fortran files and of Gfitter c++ classes involved

Gfitter/gsm/WZFitter.cxx[Goebel] <--- ZFITTER/dizet6_42.f [ZFITTER authors]
Gfitter/gsm/Z0ZFitter.cxx[Goebel, Hoecker] <--- ZFITTER/dizet6_42.f [ZFITTER authors]
Gfitter/gsm/GSMMath.cxx [Goebel] <--- ZFITTER/dizet6_42.f [ZFITTER authors] + ZFITTER/bcqcdl5_14.f [Bardin, Chizhov]
Gfitter/gsm/RadiatorFunctions.cxx[Goebel] <--- ZFITTER/dizet6_42.f [ZFITTER authors]
Gfitter/gsm/ZFitterBosonPart.cxx[Goebel, Hoecker] <--- ZFITTER/dizet6_42.f [ZFITTER authors]
Gfitter/gsm/ZFitterFermionPart.cxx[Goebel, Hoecker] <--- ZFITTER/dizet6_42.f [ZFITTER authors]
Gfitter/gsm/ZFitterQCDCorrections.cxx [Goebel, Hoecker] <--- ZFITTER/bkqcdl5_14.f [mainly B. Kniehl, a bit ZFITTER authors]
Gfitter/gsm/EW2loop.cxx[Goebel] <--- ZFITTER/m2tcor5_11.f [G. Degrassi et al.]
Gfitter/gsm/Vertex.cxx[Goebel] <--- ZFITTER/dizet6_42.f [ZFITTER authors]

The corresponding files are linked here so that the user may develop an independent opinion.
We will not discuss details of the files related to B. Kniehl and G. Degrassi et al., but give only one comment to each of them:
In ZFITTER/bkqcdl5_14.f we refer on line 2 to the "B.Kniehl QCD-library", and this comment has been deleted in Gfitter/gsm/ZFitterQCDCorrections.cxx.
In ZFITTER/m2tcor5_11.f we quote on line 95ff.: " c Dear Dima, here are the routines ... All best Giuseppe." Also this comment has been deleted in Gfitter/gsm/EW2loop.cxx.
We used the Fortran routines of both groups with the explicit, prior agreemetn of the authors.
Our quotations to Bernd Kniehl and Giuseppe Degrassi et al. in the Fortran files are not so marked, this is true, but they exist. In our CPC description of ZFITTER we write in the introduction that we have code of other authors integrated, and give there more details. In sum, it should be considered correct.

09 March 2011:
First Proof of Evidence of `integrations'
by 4 examples which were presented this date and during the days after to collegues, including some of the supporters of Gfitter --

FUNCTION XL(Q2,AM12,AM22) - line 1030 ff. in ZFITTER/dizet6_42.f
We consider here one of the many functions in Gfitter where Gfitter authors write in the code Gfitter/GSM that they have taken them from some journal publication or preprint or book, but in fact this is not true.
The example is not the simplest one, but after one catched the logics of it, it is quite convincing. It was our first observation, just by eye, not by dedicated search.
Function "L" in Gfitter/gsm [or "XL" in the original, ZFITTER/dizet] is a simple auxiliary function and appears several times in different versions. Our observations apply to other auxiliary functions, too.
In Gfitter/gsm/GSMMath.cxx, they write that this is equation (A.8) of
D. Yu. Bardin, M.S. Bilenky, G.V. Mitselmakher, T. Riemann, M. Sachwitz
"A realistic approach to the standard Z peak"
Z. Phys. C - Particles and Fields 44, 493-502 (1989)
The formula (A.8) describes a complex function. It is given a bit `generic' in the journal, does not work out in real Fortran and one has to consider several cases:

There are many ways to program this. Inspecting by eye the two codes, one gets convinced that they are not independent of each other, but one is `derived' [= `copied and changed'] from the other.

In ZFITTER/dizet6_42.f [language: Fortran]:
```
 FUNCTION XL(Q2,AM12,AM22)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      COMMON/CDZCON/PI,PI2,F1,D3,ALFAI,AL4PI,AL2PI,AL1PI
*
* XL(Q2,M12,M22)=L(Q2,M12,M22)=ALAM(Q2,-M12,-M22)*J(Q2,M12,M22)
*
      ALAM=(Q2+AM12+AM22)**2-4.D0*AM12*AM22
      REL=ALAM*FJJ(Q2,AM12,AM22)
      AIL=0.D0
      TRES=(SQRT(AM12)+SQRT(AM22))**2
      IF(-Q2.LE.TRES.OR.ALAM.LT.0D0) GO TO 1
      SLAM=SQRT(ALAM)
      AIL=2.D0*PI*SLAM
1     XL=DCMPLX(REL,AIL)
```
and in Gfitter/gsm/GSMmath.cxx [language c++]:
```
// eq. (A.8) Z. Phys. C44, 493-502 (1989) 
std::complex GSM::GSMMath::L( const Double_t& Q2, const Double_t& m12, const Double_t& m22
)
{    
   Double_t LAM = (Q2 + m12 + m22)*(Q2 + m12 + m22) - 4.0*m12*m22;
   std::complex REL = LAM*JJ(Q2,m12,m22);
   Double_t IL  = 0;
   if (-Q2 > Gfitter::GMath::IPow(sqrt(m12)+sqrt(m22),2) && LAM >= 0) IL =
2.0*TMath::Pi()*sqrt(LAM);
   std::complex l(real(REL),IL);
    
   return l;
}
```
Similarly, one might discuss equation (C.6) for the ZFITTER function XJ:

Etc.

FUNCTION XDL(Q2,Q2SBT,AM12,AM22) - line 981 ff. in ZFITTER/dizet6_42.f
The next function stands for many similar cases of quite different complexity.
These function have in Gfitter no quotation to some publication, but one may find them just in ZFITTER.

In ZFITTER/dizet6_42.f [language: Fortran]:

     FUNCTION XDL(Q2,Q2SBT,AM12,AM22)
*
* XDL(Q2,AMQ2,AM12,AM22)=(L(Q2,AM12,AM22)-L(Q2SBT,AM12,AM22))/(Q2-Q2SBT)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      DATA EPS/1.D-3/
*
      Q2S=Q2SBT+AM12+AM22
      ALAM=Q2S**2-4.D0*AM12*AM22
      DSLAM=DSQRT(DABS(ALAM))
      QD=Q2-Q2SBT
      RQD=DABS(QD/DSLAM)
      IF(RQD.LE.EPS) GO TO 1
      XDL=(XL(Q2,AM12,AM22)-XL(Q2SBT,AM12,AM22))/QD
      RETURN
1     R=4.D0*AM12/AM22
      IF(R-1.D0)2,3,2
2     XJS=XJ(Q2SBT,AM12,AM22)
      XDL=2.D0+Q2S*XJS+QD/ALAM*(Q2S-2.D0*AM12*AM22*XJS)
     *   +(QD/ALAM)**2*(-Q2S**2/3.D0-8.D0/3.D0*AM12*AM22*Q2S*XJS)
      RETURN
3     CONTINUE
      RAT=QD/AM22
      XDL=4.D0+2.D0/3.D0*RAT-2.D0/15.D0*RAT*RAT
*
      END

and in Gfitter/gsm/GSMmath.cxx [language c++]:

// Delta L
std::complex GSM::GSMMath::DL( const Double_t& Q2, const Double_t& Q2SBT, const Double_t&
m12, const Double_t& m22 )
{
   std::complex dl(0,0);
   Double_t Q2S   = Q2SBT + m12 + m22;
   Double_t LAM   = Q2S*Q2S - 4.0*m12*m22;
   Double_t SLAM  = TMath::Sqrt(TMath::Abs(LAM));
   Double_t QD    = Q2 -Q2SBT;
   Double_t RQD   = TMath::Abs(QD/SLAM);
   if (RQD < 1e-3) {
      Double_t R = 4.0*m12/m22;
      if (R-1.0 != 0) {
         std::complex JS = J(Q2SBT,m12,m22);
         dl = ( 2.0 + Q2S*JS + QD/LAM*(Q2S - 2.0*m12*m22*JS) 
                + (QD/LAM)*(QD/LAM)*(-Q2S*Q2S/3.0 - 8.0/3.0*m12*m22*Q2S*JS) );
      }
      else dl = 4.0 + 2.0/3.0*QD/m22 - 2.0/15.0*QD*QD/(m22*m22);
   }
   else dl = (L(Q2,m12,m22) - L(Q2SBT,m12,m22))/QD;

   return dl;
}

FUNCTION XAMF(Q2) - line 1329 ff. in ZFITTER/dizet6_42.f
We identified 12 cases where a quotation to ZFITTER/dizet6_42.f is given, usually with a line number which agrees with the one we identify in our copy of dizet6_42.f. Even if there is mentioned in addition a reference to some publication, the software was nevertheless used for the code `integration'.
A nice sample is "FUNCTION XAMF(Q2)".

In ZFITTER/dizet6_42.f [language: Fortran]:

      FUNCTION XAMF(Q2)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
      COMMON/CDZWSM/AMW2,AMZ2,R,R1,R12,R2,AMH2,RW,RW1,RW12,RW2,RZ,RZ1,
     *      RZ12,RZ2,ALR,ALRW,ALRZ,SW2M,CW2M,AKSX,R1W,R1W2
      COMMON/CDZFER/CLM(8),AML(8),CQM(8),AMQ(8),VB,VT,VB2,VB2T,VT2,VT2T
*
      NG=3
      XCHMQ1=DCMPLX(0.D0,0.D0)
      DO 1 I=1,NG
      AML2=AML(2*I)**2
      XCHMQ1=XCHMQ1+XI3(AMW2,Q2,AML2,AML2)
1     CONTINUE
      XCHQ21=XCHMQ1
* equal for leptons
      INQ=2*NG
      DO 2 I=1,INQ
      AMQ2=AMQ(I)**2
      XCHMQ1=XCHMQ1+3.D0*CQM(I)*XI3(AMW2,Q2,AMQ2,AMQ2)
      XCHQ21=XCHQ21+3.D0*CQM(I)**2*XI3(AMW2,Q2,AMQ2,AMQ2)
2     CONTINUE
      XAMF=8.D0*R1*XCHQ21-2.D0*XCHMQ1
*
      END

and in Gfitter/gsm/ZFitterFermionPart.cxx [language c++]:

// eq. (264) of hep-ph/9709229v1 
// see ZFitter package dizet6_42.f line 1329-1352 ( function XAMF )
complex GSM::ZFitterFermionPart::MfphoZ( const Double_t& Q2 ) const
{    
   complex chmQ1 (0,0);
   
   // leptons
   for (Int_t i=0; i<3 ; i++) {
      Double_t ml2 = m_ml[1][i]*m_ml[1][i];
      chmQ1 = chmQ1 + GSMMath::I3(m_MW2, Q2, ml2, ml2);
   }

   complex chmQ2 = chmQ1;

   // quarks
   for (Int_t i=0; i<3; i++) {
      for (Int_t j=0; j<2; j++) {
         Double_t mq2 = m_mq[j][i]*m_mq[j][i];
         chmQ1  = chmQ1 + 3.0*m_chq[j]*GSMMath::I3(m_MW2, Q2, mq2, mq2);
         chmQ2  = chmQ2 + 3.0*m_chq[j]*m_chq[j]*GSMMath::I3(m_MW2, Q2, mq2, mq2);
      }
   }
   return 8.0*m_R1*chmQ2 - 2.0*chmQ1;
}

The hint in the c++ code to "// eq. (264) of hep-ph/9709229v1" is not a hint to the source of its programming, but just links informal to the reference.
In this reference, section 4.4. "ZFITTER basics", authored by D. Bardin, M. Bilenky, S. Riemann, T. Riemann, the function "I3(−s;mf2,mf2)" has 3 arguments. It is interesting to notice that this function has 4 arguments in both codes.
The reasons are simple.
In ZFITTER, it has purely historical reasons, in the description, eq. (264) we left the useless 4^th argument out, and in Gfitter/GSM it was just copied from ZFITTER without too much reasoning.
If the article would have been source for coding in Gfitter/GSM, we would meet there the "I3" with 3 arguments only.

The m_t^4 corrections for arbitrary values of the Higgs mass due to R. Barbieri et al.
In ZFITTER/dizet6_42.f, all the m_t^4 radiative correction effects to the electroweak precision observables for arbitrary values of the Higgs mass are evaluated following:

R. Barbieri, M. Beccaria, P. Ciafaloni, G. Curci and A. Viceré, "Two-loop heavy-top effects in the Standard Model", Nucl. Phys. B409 (1993) 105-127

The coding in ZITTER/dizet6_42.f: 2 functions, FBARB(X) and FBARBB(X). The first one is:

ZFITTER/dizet6_42.f, lines 4547 ff.

      FUNCTION FBARB(X)
      IMPLICIT REAL*8(A-Z)
      COMMON/CDZCON/PI,PI2,F1,D3,ALFAI,AL4PI,AL2PI,AL1PI
      DATA P1/-0.74141D0/,P2/ -11.483D0  /,P3/  9.6577D0/,
     &     P4/ -6.7270D0/,P5/  3.0659D0  /,P6/-0.82053D0/,
     &     P7/ 0.11659D0/,P8/-0.67712D-02/
      IF(X.LE.4D0) THEN
        FBARB=P1+P2*X+P3*X**2+P4*X**3+P5*X**4+P6*X**5+P7*X**6+P8*X**7
         ELSE
        RBTH=1/X**2
        ALRB=LOG(RBTH)
        FBARB=49D0/4D0+PI2+27D0/2D0*ALRB+3D0/2D0*ALRB**2
     &       +RBTH/3D0*(2D0-12D0*PI2+12D0*ALRB-27D0*ALRB**2)
     &       +RBTH**2/48D0*(1613-240*PI2-1500*ALRB-720 *ALRB**2)
      ENDIF
*
      END

The Barbieri et al. implementations are unpublished outside the software package ZFITTER/dizet. They arose and were tested in close cooperation of D. Bardin with R. Barbieri et al., as is also acknowledged in the publication of Barbieri et al.
In 2006, the ZFITTER coding has been `integrated' into GSMMath.cxx

Gfitter/GSM/GSMMATH.cxx, lines 266 ff.

// mtop^4 contribution from Barbieri et. al.      
// Nucl. Phys. B409(1993) 105-107
Double_t GSM::GSMMath::BarbMc( const Double_t& x )
{  
   Double_t P[8] = {-0.74141, -11.483, 9.6577, -6.727, 3.0659, -0.82053, 0.11659, -0.67712e-2};
   Double_t Barb = 0;
   if (x < 4) {
      for (Int_t i = 0; i < 8; i++) {  Barb += P[i]*Gfitter::GMath::IPow(x,i); }
   }
   else {
      Double_t Pi2      = Gfitter::GMath::IPow(TMath::Pi(),2);
      Double_t Inv2     = 1/(x*x);
      Double_t LogInv2  = TMath::Log(Inv2);
      Barb              = ( 49/4.0 + Pi2 + 27/2.0*LogInv2 + 3/2.0*LogInv2*LogInv2
                            + Inv2/3.0*(2.0 - 12.0*Pi2 + 12.0*LogInv2 -27.0*LogInv2*LogInv2)
                            + Inv2*Inv2/48.0*(1613.0 - 240.0*Pi2 - 1500.0*LogInv2 -
720.0*LogInv2*LogInv2) );
   }
   return Barb;
}

The paper by R. Barbieri et al., Nuclear Physics B409 (1993) 105—127 does not contain this formula or the next one. They were programmed and tested in close cooperation with R. Barbieri et al., as is also acknowledged in their publication.
The other formula related to that:

ZFITTER/dizet6_42.f, lines 4565 ff

      FUNCTION FBARBB(X)
C 13/10/1992 - Barbieri's m_t^4 are implemented
      IMPLICIT REAL*8(A-Z)
      COMMON/CDZCON/PI,PI2,F1,D3,ALFAI,AL4PI,AL2PI,AL1PI
* Approximation from 0 to 4 (Mhiggs/mtop)
      DATA P1/ 5.6807D0/,P2/ -11.015D0  /,P3/ 12.814D0/,
     &     P4/-9.2954D0/,P5/  4.3305D0  /,P6/-1.2125D0/,
     &     P7/0.18402D0/,P8/-0.11582D-01/
      IF(X.LE.4D0) THEN
        FBARBB=P1+P2*X+P3*X**2+P4*X**3+P5*X**4+P6*X**5+P7*X**6+P8*X**7
         ELSE
        RBTH=1/X**2
        ALRB=LOG(RBTH)
        FBARBB=1D0/144*(311D0+24*PI2+282*ALRB+90*ALRB**2
     &        -4D0*RBTH*(40D0+ 6*PI2+ 15*ALRB+18*ALRB**2)
     &        +3D0*RBTH**2*(242.09D0-60*PI2-454.2D0*ALRB-180*ALRB**2))
      ENDIF
*
      END

and in Gfitter:

Gfitter/GSM/GSMMATH.cxx, lines 287 ff.

{  
   Double_t P[8] = {5.6807, -11.015, 12.814, -9.2954, 4.3305, -1.2125, 0.18402, -0.11582e-1};
   Double_t Barb = 0;
   if (x < 4) {
      for (Int_t i = 0; i < 8; i++) {  Barb += P[i]*Gfitter::GMath::IPow(x,i); }
   }
   else {
      Double_t Pi2      = Gfitter::GMath::IPow(TMath::Pi(),2);
      Double_t Inv2     = 1/(x*x);
      Double_t LogInv2  = TMath::Log(Inv2);
      Barb              = 1/144.0*( 311.0 + 24.0*Pi2 + 282.0*LogInv2 + 90.0*LogInv2*LogInv2
                                    - 4.0*Inv2*(40.0 + 6.0*Pi2 + 15.0*LogInv2 + 18.0*LogInv2*LogInv2)
                                    + 3.0*Inv2*Inv2*(242.09 - 60.0*Pi2 - 454.2*LogInv2 - 180.0*LogInv2*LogInv2) );
   }
   return Barb;
}

Without mentioning by Gfitter that the coding follows ZFITTER. But by inspection it becomes evident that the source is ZFITTER/dizet6_42.f.

After 09 March 2011, a lot of more `integrations' by Gfitter authors have been made evident by us.

Since 11 May 2011:
Additional Evidence of `integrations'
by examples presented to Gfitter representatives, supporters and `experts'

The one-loop electroweak corrections to the W decay width
Details of comparison are shown here.
Some comments:
The first calculation of the one-loop corrections to the W decay width in the Standard Model of the Dubna group was done in:
"Electroweak One Loop Corrections To The Decay Of The Charged Vector Boson"
D.Yu. Bardin, S. Riemann, T. Riemann (Dubna, JINR)
ZFPC32 (1986) [preprint JINR-E2-86-169].
We did the calculation with inclusion of the heavy top quark corrections. The main part of the form factor is eq. (A.5):

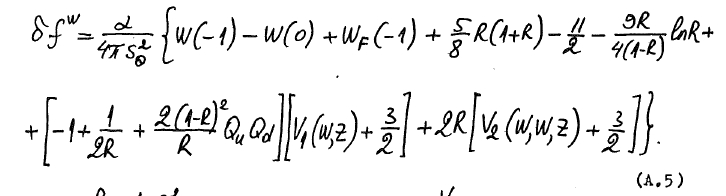
e2-86-169-bardin-riemann-riemann-A5

This was the original basis of "SUBROUTINE PROW", which calculates function "ROW" and found its way into all the versions of ZFITTER/dizet.

      SUBROUTINE PROW (QI,ROW)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
      COMMON/CDZCON/PI,PI2,F1,D3,ALFAI,AL4PI,AL2PI,AL1PI
      COMMON/CDZWSM/AMW2,AMZ2,R,R1,R12,R2,AMH2,RW,RW1,RW12,RW2,RZ,RZ1,
     *      RZ12,RZ2,ALR,ALRW,ALRZ,SW2M,CW2M,AKSX,R1W,R1W2
      COMMON/CDZWSC/SL2,SQ2,W0,W0F,Z0,Z0F,DWZ0R1,DWZ0F,XWM1,XWM1F,XZM1,
     &      XZM1F,XWZ1R1,XDWZ1F,XZFM1,XZFM1F,XAMM1,XAMM1F,XWFM1,XWFM1F
      COMMON/CDZVZW/V1ZZ,V1ZW,V2ZWW,V1WZ,V2WWZ,VTB
*
      QIQJ=QI*(1.D0-QI)
      WM1A=DREAL(XWM1+XWM1F)
      W0A=W0+W0F
      WFM1A=DREAL(XWFM1+XWFM1F)
      ROW=1.D0+AL4PI/R1*(WM1A-W0A+WFM1A-7.D0/1.D0+5.D0/8.D0*R*R1W
     *   -9.D0/4.D0*R/R1*ALR+3.D0/4.D0/R+3.D0*R-3.D0/R*R12*QIQJ
     *   +(1.D0/2.D0/R-1.D0-2.D0*R12/R*QIQJ)*V1WZ
     *   +2.D0*R*V2WWZ+2.D0*R1*(77.D0/12.D0-2.D0/3.D0*PI2+109.D0/36.D0
     *   -3.D0/2.D0*QIQJ))
      PROW1=100.D0*(ROW-1.D0)
*
      END

In Gfitter/gsm/WZFitter.cxx, this is `integrated' as function "rho".

// rho for W decay, just 1-loop, because it is impossible 
// to define QED-gauge invariant subset of diagrams
Double_t GSM::WZFitter::GetRhoW( Double_t Charge )
{
   Update();
   Double_t ChUpDo = Charge*(1.0 - Charge);
   
   // eq. (10.71) of The Standard Model in the Making
   // one and two point functions are replaced
   // by fermionic and bosonic contribution
   Double_t rho    = ( 1.0 + GConstants::alphaQED()/(4.0*TMath::Pi()*(1.0-m_R))
                       *(m_W_MW - m_W0 + m_WF_MW - 7.0 + 5/8.0*m_R*(1.0+m_R) 
                         - 9/4.0*m_R/(1.0-m_R)*TMath::Log(m_R) 
                         + 0.75/m_R + 3.0*m_R - 3.0/m_R*(1.0-m_R)*(1.0-m_R)*ChUpDo
                         + (0.5/m_R - 1.0 -
2.0*(1.0-m_R)*(1.0-m_R)/m_R*ChUpDo)*GetVertex().GetV1WZ()
                         + 2.0*m_R*GetVertex().GetV2WWZ() + 2.0*(1.0-m_R)
                         *(77/12.0 - 2/3.0*GMath::IPow( TMath::Pi(),2 ) + 109/36.0 - 3/2.0*ChUpDo))
);
   return rho;
}

The files demonstrate nicely that even the order of terms and some linebreaks agree, while the names of variables have been changed systematically.
The comment line in Gfitter/gsm/WZFitter.cxx

   // eq. (10.71) of The Standard Model in the Making
   // one and two point functions are replaced
   // by fermionic and bosonic contribution

suggests that the formula for "rho" is taken from the monography by D. Bardin, G. Passarino, "The Standard Model in the Making" (Oxford, UK: Clarendon (1999) 685 p.), but this is not the case:

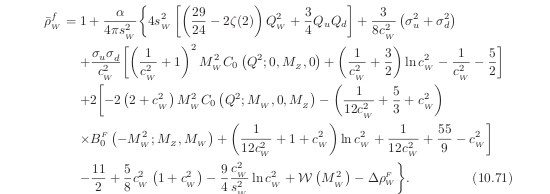
eq-10.71-of-standard-model-in-the-making

eq-10.71-of-standard-model-in-the-making

1270 or 127 ?
See RadiatorFunctions-detailed.pdf for more details.
A subtle example of hidden code `integrations' is the QCD coefficient C_{23}^A, calculated in Gfitter/GSM/RadiatorFunctions.cxx. They quote at the begin of file:

* Description:                                                                   *
 *      Auxiliary Theory computes QCD radiator functions                          *
 *      for Z and W decay                                                         *
 *                                                                                *
 * Papers:                                                                        *
 *      The Standard Model in the Making, Oxford 1999                             *
 *                                                                                *
 * Authors (alphabetical):                                                        *
 *      Martin Goebel     - DESY, Germany

In fact, in the book you find:
RadiatorFunctions-sm-making-p505-eq12_38-c23a

Accordingly, the formula in Mr. Goebel's diploma thesis is
RadiatorFunctionsGoebel_dipl-p85-c23A-

and in the Gfitter article EPJC 60:
RadiatorFunctionsGoebel_dipl-p85-c23A-

The coefficient of zeta(5) in all these expressions is "127".
In Gfitter/GSM/RadiatorFunctions.cxx one reads instead "1270 zeta(5)":


RadiatorF:   // axial part
RadiatorF:    m_CA0   = -6.0;
RadiatorF:    m_CA1   = -22.0;
RadiatorF:    m_CA2   = -8221/24.0 + 57*zeta2 + 117*zeta3 + (151/12.0 - 2*zeta2 - 4*zeta3)*m_nf1;
RadiatorF:    m_CA3   = ( - 4544045/864.0 + 1340*zeta2 + 118915/36.0*zeta3 - 1270*zeta5
RadiatorF:                + (71621/162.0 - 209/2.0*zeta2 - 216*zeta3 + 5*zeta4 + 55*zeta5)*m_nf1
RadiatorF:                + (-13171/1944.0 + 16/9.0*zeta2 + 26/9.0*zeta3)*m_nf1*m_nf1 );

This is not a typo as one might assume, because a look into ZFITTER/dizet6_42.f shows that this and related functions are just copied from there and then by re-namings adapted, without mentioning this:


dizet: *
dizet:       COEFA0=-6D0
dizet:       COEFA1=-22D0
dizet:       COEFA2=-8221D0/24+57D0*D2+117D0*D3
dizet:      &      +(151D0/12 - 2D0*D2-  4D0*D3)*ANF   
dizet:       COEFA3=-4544045D0/864+   1340*D2+118915D0/36*D3  -1270D0*D5
dizet:      &      +(71621D0/162  -209D0/2*D2   -216D0*D3+5D0*D4+55D0*D5)*ANF
dizet:      &      +(-13171D0/1944+ 16D0/9*D2  +26D0/9*D3            )*ANF**2
dizet: *

Since the corresponding formulae in the book are typed by `latexization' of the existing Fortran, they look quite similar, and if then the latex would have been - legally because quoted - `c++ - ized', one would get what is in Gfitter/GSM/RadiatorFunctions.cxx. But, the typo in the book was taken into the Gfitter texts, but not into the gfitter software. In a discussion with Gfitter people we made evident that they were not even aware of the 127 - 1270 mismatch.

Vertex functions for W and Z decays
See Vertex-detailed.pdf for more details.

Compare to the discussion on "The "bible", rho, kappa, uff, V1ZZ, V1ZW, V2ZWW, and all that" for Latex aspects.
Some bosonic self-energy contributions for W and Z decays
See ZFitterBosonPart-detailed.pdf for more details.

Compare to the discussion on "The "bible", rho, kappa, uff, V1ZZ, V1ZW, V2ZWW, and all that" for Latex aspects.
Some fermionic self-energy contributions for W and Z decays
See ZFitterFermionPart-detailed.pdf for more details.

Compare to the discussion on "The "bible", rho, kappa, uff, V1ZZ, V1ZW, V2ZWW, and all that" for Latex aspects.

ZFITTER/bcqcdl5_14.f: QCD corrections a la D. Bardin, A. Chizhov
In file ZFITTER/bcqcdl5_14.f there are correction derived in
D. Bardin and A. Chizhov, "On the O(alpha_em alpha_s) corrections to electroweak observables", in: JINR preprint E2-89-525 (1989) p.42-48, Proc. Int. Topical Seminar on Physics of e+e- Interactions at LEP energies, JINR, Dubna, 15-16 Nov 1988.
see also: ZFITTER description, CPC 133, section 3.4.1.
The expressions are a Fortran implementation of results published in A. Djouadi, C. Verzegnassi, PLB 195 (1987) 265.
Parts of the file have been `integrated' into Gfitter/GSM/GSMMath.cxx without mentioning. The implementation has certainly never been used.
ZFITTER/bcqcdl5_14.f: QCD corrections a la Bardin/Chizhov

      FUNCTION XPVFI(AL)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      RPVFI=45.D0/4.D0/AL-82.D0/27.D0/AL**2+449.D0/900.D0/AL**3
     *     -62479.D0/661500.D0/AL**4
      XPVFI=DCMPLX(RPVFI,.0D0)
*
      END

While in Gfitter:

gsmmath l. 377 ff.

// some polarization operators and their auxiliary functions

complex GSM::GSMMath::PolVfi( const Double_t& al )
{
   return ( 45.0/(4.0*al) - 82.0/(27.0*al*al) + 449.0/(900.0*al*al*al)
            - 62479.0/(661500.0*al*al*al*al) );
}

The next pair of functions:

         FUNCTION XPAFI(AL)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      RPAFI=-93.D0/2.D0+67.D0/12.D0/AL-689.D0/540.D0/AL**2
     *     +1691.D0/12600.D0/AL**3-1.8599D-2/AL**4
      XPAFI=DCMPLX(RPAFI,.0D0)
*
      END

and

complex GSM::GSMMath::PolAfi( const Double_t& al )
{    
   return ( -93.0/2.0+67.0/12.0/al-689.0/540.0/(al*al)
            +1691.0/12600.0/(al*al*al)-1.8599e-2/(al*al*al*al) );
}

The next pair of functions:

      FUNCTION XDPVFI(AL)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      RDPVFI=45.D0/4.D0-164.D0/27.D0/AL+449.D0/300.D0/AL**2
     *      -62479.D0/165375.D0/AL**3+9.55063D-2/AL**4
      XDPVFI=DCMPLX(RDPVFI,.0D0)
*
      END

and in GSMMATH:

complex GSM::GSMMath::DPolVfi( const Double_t& al )
{
   return ( 45.0/4.0 - 164.0/(27.0*al) + 449.0/(300.0*al*al)
            - 62479.0/(165375.0*al*al*al) + 9.55063e-2/(al*al*al*al) );
}

The next pair of functions:

        FUNCTION XDPAFI(AL)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      RDPAFI=67.D0/12.D0-689.D0/270.D0/AL+1691.D0/4200.D0/AL**2
     *      -7.43961D-2/AL**3+275205680132.D0/18606865047887.D0/AL**4
      XDPAFI=DCMPLX(RDPAFI,.0D0)
*
      END

and

complex GSM::GSMMath::DPolAfi( const Double_t& al )
{
   return ( 67.0/12.0-689.0/270.0/al+1691.0/4200.0/(al*al)
            -7.43961e-2/(al*al*al)+275205680132.0/18606865047887.0/(al*al*al*al) );
}

FUNCTION AFMT3(ALST,AMT2,AMZ2,SW2) - line 5484 ff. in ZFITTER/dizet6_42.f
The corrections are based on L. Avdeev (Dubna, JINR), J. Fleischer (Bielefeld U.), S. Mikhailov (Dubna, JINR), O. Tarasov (Bielefeld U.), "O(alpha alpha_s^2) correction to the electroweak rho parameter", Phys. Lett. B 336 (1994) 560–566, e-Print: hep-ph/9406363;
The code of this function with all its parts and intermediate functions is `integrated' from ZFITTER/dizet into Gfitter/GSM/GSMMath.cxx.

Look e.g. at the three constants evaluated in the article with 19 digits or more:

S_2 = 0.260 434 137 632 162 098 955 729
D_3 = −3.027 009 493 987 652 019 786
B_4 = −1.762 800 087 073 770 086

In ZFITTER/dizet they are renamed and a bit shortened [T for Tarasov, but I have no idea why here shortened to 13 digits after the comma]

TS2=+0.2604341376322D0
TD3=-3.0270094939877D0
TB4=-1.7628000870738D0

In Gfitter/GSM/GSMMath.cxx they appear identical to ZFITTER, and the specific form was never published by us. So, let us assume they were `integrated' from the Fortran source:
gsm/ .....
Double_t TS2 = 0.2604341376322;
Double_t TD3 = -3.0270094939877;
Double_t TB4 = -1.7628000870738;

The complete function is:

ZFITTER/dizet6_42.f, lines 5484 ff.

      FUNCTION AFMT3(ALST,AMT2,AMZ2,SW2)
*
      IMPLICIT REAL*8(A-H,O-Z)
*
      COMMON/CDZSCT/ISCRE,ISCAL,IAFMT,IFACR,IFACT,IHIGS,IEWLC,ICZAK
     &             ,IHIG2,IALE2,IGFER      
*
* NUMERICAL CONSTANTS
*
      PI=ATAN(1D0)*4D0
      PI2=PI**2
      D2=PI2/6D0
      D3=1.2020569031596D0
      D4=PI2**2/90
      AL2=LOG(2D0)
      TS2=+0.2604341376322D0
      TD3=-3.0270094939877D0
      TB4=-1.7628000870738D0
      AMU2=AMT2
      ALMU=LOG(AMU2/AMT2)
      NF=6
      CA1=-2D0/3*(1+2*D2)
      CA2L=157D0/648-3313D0/162*D2-308D0/27*D3+143D0/18*D4-4D0/3*D2*AL2
     & +441D0/8*TS2-1D0/9*TB4-1D0/18*TD3-(1D0/18-13D0/9*D2+4D0/9*D3)*NF
     & -(11D0/6-1D0/9*NF)*(1+2*D2)*ALMU
      ALZT=LOG(AMZ2/AMT2)
      CA2C=AMZ2/AMT2*(-17.2240D0+0.08829D0*ALZT+0.4722D0*ALZT**2
     &               +(22.6367D0+1.25270D0*ALZT-0.8519D0*ALZT**2)*SW2)
      CA2I=(AMZ2/AMT2)**2*(-7.7781D0-0.072263D0*ALZT+0.004938D0*ALZT**2+
     &(21.497D0+0.05794D0*ALZT-0.006584D0*ALZT**2)*SW2-21.0799D0*SW2**2)
      IF(IAFMT.EQ.1) CA2=CA2L
      IF(IAFMT.EQ.2) CA2=CA2L+CA2C
      IF(IAFMT.EQ.3) CA2=CA2L+CA2C+CA2I
      AFMT3=CA1*ALST/PI+CA2*(ALST/PI)**2
*
      END

This is to be compared with:

Gfitter/GSM/GSMMATH.cxx, lines 337 ff.:

Double_t GSM::GSMMath::Afmt3( const Double_t& alst, const Double_t& mt2, const Double_t& MZ2, const
Double_t& sW2 )
{
   Double_t TS2   =  0.2604341376322; 
   Double_t TD3   = -3.0270094939877;
   Double_t TB4   = -1.7628000870738;
   Double_t LogZT =  TMath::Log(MZ2/mt2);
   Int_t nf       =  6;

   Double_t CA1   = -2/3.0*(1.0 + 2*Gfitter::GMath::Zeta2());
   Double_t CA2C  = ( MZ2/mt2*(-17.224 + 0.08829*LogZT + 0.4722*LogZT*LogZT
                               + ( 22.6367 + 1.2527*LogZT - 0.8519*LogZT*LogZT)*sW2) );
   Double_t CA2L  = ( 157/648.0 - 3313/162.0*Gfitter::GMath::Zeta2() - 308/27.0*Gfitter::GMath::Zeta3()
                      + 143/18.0*Gfitter::GMath::Zeta4() - 4/3.0*Gfitter::GMath::Zeta2()*TMath::Log(2.0)
                      + 441/8.0*TS2 - 1/9.0*TB4 - 1/18.0*TD3 
                      - (1/18.0 - 13/9.0*Gfitter::GMath::Zeta2() + 4/9.0*Gfitter::GMath::Zeta3())*nf
);
   // - (11/6.0 - 1/9.0*nf)*(1.0 + 2*Gfitter::GMath::Zeta2())*TMath::Log(mt2/mt2)
   Double_t CA2I  = ( Gfitter::GMath::IPow(MZ2/mt2,2)*
                      (-7.7781 - 0.072263*LogZT + 0.004938*LogZT*LogZT
                       + (21.497 + 0.05794*LogZT - 0.006584*LogZT*LogZT)*sW2 - 21.0799*sW2*sW2) );

   Double_t CA2   = CA2L + CA2C + CA2I;
	  
   return CA1*alst/TMath::Pi() + CA2*Gfitter::GMath::IPow( alst/TMath::Pi() ,2 );
}

S3WANA In ZFITTER/dizet lines4036 ff.:

    SUBROUTINE S3WANA(MT2,MW2,AMQ2,J0,S3,S30)
*
* Supplies real parts of J0,S3,S30 (w,t) in analytic presentation
* CALL S3ANA(MT2,MW2,-S,...) supplies `w' indices
* CALL S3ANA(MW2,MT2,-S,...) supplies `t' indices
*
      IMPLICIT NONE
      REAL*8 MT2,MW2,AMQ2
      REAL*8 PI,PI2,D2,D3,ALFAI,AL4PI,AL2PI,AL1PI
      COMPLEX*16 AMT2,AMW2
      COMPLEX*16 SQR,LQR,X0,X1,X2,X3
      COMPLEX*16 Y1,Y2,Y3,Y4,Y5,Y6,J0,S3,S30
      COMPLEX*16 XSPENZ,LOG,SQRT
c      COMPLEX*16 A1,A2,A3,A4,A5,A6
*
      COMMON/CDZCON/PI,PI2,D2,D3,ALFAI,AL4PI,AL2PI,AL1PI
*
      AMT2=DCMPLX(MT2,-1D-10)
      AMW2=DCMPLX(MW2,-1D-10)
*
      SQR=SQRT(1D0+4D0*AMW2/AMQ2)
*
      LQR=LOG((SQR+1D0)/(SQR-1D0))
      J0 =SQR*LQR
      IF(MT2.GT.MW2) THEN
        S30=1D0/AMQ2*LQR**2
      ELSE
        S30=1D0/AMQ2*(D2-XSPENZ(1D0-AMQ2/AMT2))
      ENDIF
*
      X1=(1D0-SQR)/2D0
      X2=(1D0+SQR)/2D0
      X0=(AMT2-AMW2)/AMQ2
      X3=AMT2/(AMT2-AMW2)
*
      Y1=X1/X0
      Y2=(1D0-X1)/(1D0-X0)
      Y3=X2/X0
      Y4=(1D0-X2)/(1D0-X0)
      Y5=X3/X0
      Y6=(1D0-X3)/(1D0-X0)
*
c      A1=1D0/(1D0-Y1)
c      A2=1D0/(1D0-Y2)
c      A3=1D0/(1D0-Y3)
c      A4=1D0/(1D0-Y4)
c      A5=1D0/(1D0-Y5)
c      A6=1D0/(1D0-Y6)
*
      S3=1D0/AMQ2*(XSPENZ(1D0/(1D0-Y1))-XSPENZ(1D0/(1D0-Y2))
     &            +XSPENZ(1D0/(1D0-Y3))-XSPENZ(1D0/(1D0-Y4))
     &            -XSPENZ(1D0/(1D0-Y5))+XSPENZ(1D0/(1D0-Y6)))
c      S3=1D0/AMQ2*(XSPENZ(A1)-XSPENZ(A2)
c     &            +XSPENZ(A3)-XSPENZ(A4)
c     &            -XSPENZ(A5)+XSPENZ(A6))
*
      RETURN
      END

and in Gfitter/GSM/GSSMATH.cxx:

// Supplies real parts of J0,S3,S30 (w,t) in analytic presentation
// S3Wana(mt2,MW2,-s,...) supplies `w' indices
// S3Wana(MW2,mt2,-s,...) supplies `t' indices
void GSM::GSMMath::S3Wana ( const Double_t& mt2, const Double_t& MW2, const Double_t& s,
                            Double_t& J0, Double_t& S3, Double_t& S30 )
{
   std::complex Cmt2 (mt2, -1e-10);
   std::complex CMW2 (MW2, -1e-10);
   std::complex Sqrt = std::sqrt( 1.0 + 4.0*CMW2/s );
   std::complex LogS = Gfitter::GMath::Log( (Sqrt + 1.0)/(Sqrt - 1.0) );
	
   std::complex x0   = (Cmt2 - CMW2)/s;
   std::complex x1   = 0.5*(1.0 - Sqrt);
   std::complex x2   = 0.5*(1.0 + Sqrt);
   std::complex x3   = Cmt2/(Cmt2 - CMW2);

   std::complex y1   = x1/x0;
   std::complex y2   = (1.0 - x1)/(1.0 - x0);
   std::complex y3   = x2/x0;
   std::complex y4   = (1.0 - x2)/(1.0 - x0);
   std::complex y5   = x3/x0;
   std::complex y6   = (1.0 - x3)/(1.0 - x0);
	 
   // results
   J0                    = real( Sqrt*LogS );
   if (mt2 >= MW2) S30 = real( 1.0/s*LogS*LogS );
   else            S30 = real( 1.0/s*(Gfitter::GMath::Zeta2() - Gfitter::GMath::Li2(1.0 - s/mt2)) );
   S3                  = real( 1.0/s*( + Gfitter::GMath::Li2( 1.0/(1.0-y1) ) - Gfitter::GMath::Li2(1.0/(1.0-y2) ) 
                                       + Gfitter::GMath::Li2( 1.0/(1.0-y3) ) - Gfitter::GMath::Li2(1.0/(1.0-y4) ) 
                                       - Gfitter::GMath::Li2( 1.0/(1.0-y5) ) + Gfitter::GMath::Li2(1.0/(1.0-y6) ) ) );
 
}







TBQCDR

In ZFITTER/dizet lines 5521 ff.:



      FUNCTION TBQCDR(ALST,AMT2,AMZ2,SW2)
*
      IMPLICIT REAL*8(A-H,O-Z)
*
      COMMON/CDZSCT/ISCRE,ISCAL,IAFMT,IFACR,IFACT,IHIGS,IEWLC,ICZAK
     &             ,IHIG2,IALE2,IGFER      
*
* NUMERICAL CONSTANTS
*
      PI=ATAN(1D0)*4D0
      CW2=1D0-SW2
*
      ALZT=LOG(AMZ2/AMT2)
      CA2C=AMZ2/AMT2*(
     &             +(-11.3184D0-0.62630D0*ALZT+0.4259D0*ALZT**2)*SW2
     &             +(+22.6367D0+1.25270D0*ALZT-0.8519D0*ALZT**2)*SW2)
      CA2I=(AMZ2/AMT2)**2*(
     &(-16.01860-0.02897D0*ALZT+0.003292D0*ALZT**2)*SW2+10.54D0*SW2**2+
     &(21.497D0+0.05794D0*ALZT-0.006584D0*ALZT**2)*SW2-21.0799D0*SW2**2)
      IF(IAFMT.EQ.1) CA2=0D0
      IF(IAFMT.EQ.2) CA2=CA2C
      IF(IAFMT.EQ.3) CA2=CA2C+CA2I
      TBQCDR=-CW2/SW2*CA2*(ALST/PI)**2
*
      END

and in Gfitter/GSM/GSSMATH.cxx:



Double_t GSM::GSMMath::TbQCD( const Double_t& alst, const Double_t& mt2, const Double_t& MZ2, const Double_t& sW2 )
{
   Double_t cW2   = 1.0 - sW2;
   Double_t logzt = TMath::Log( MZ2/mt2);
  
   Double_t Ca2c  = ( MZ2/mt2*( +(-11.3184 - 0.62630*logzt + 0.4259*logzt*logzt)*sW2
                                +(+22.6367 + 1.25270*logzt - 0.8519*logzt*logzt)*sW2) );
   Double_t Ca2i  = ( GMath::IPow( (MZ2/mt2), 2 )*( (-16.01860 - 0.02897*logzt + 0.003292*logzt*logzt)*sW2 
                                                    + 10.54*sW2*sW2 
                                                    + (21.497 + 0.05794*logzt - 0.006584*logzt*logzt)*sW2 -
21.0799*sW2*sW2) );
 
   return -cW2/sW2*(Ca2c + Ca2i)*GMath::IPow( (alst/TMath::Pi()), 2 );
}









The "bible", rho, kappa, uff, V1ZZ, V1ZW, V2ZWW, and all that

Some vertex functions have been a bit re-arranged when they were taken over.

In ZFITTER/dizet:



      SUBROUTINE VERTZW(MZ,INDF,V_TB)
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      COMMON/CDZCON/PI,PI2,F1,D3,ALFAI,AL4PI,AL2PI,AL1PI
      COMMON/CDZWSM/AMW2,AMZ2,R,R1,R12,R2,AMH2,RW,RW1,RW12,RW2,RZ,RZ1,
     *      RZ12,RZ2,ALR,ALRW,ALRZ,SW2M,CW2M,AKSX,R1W,R1W2
      COMMON/CDZVZW/V1ZZ,V1ZW,V2ZWW,V1WZ,V2WWZ,VTB
*
      IF(MZ) 5,8,5
*
* Z-BOSON CHAIN *********************
* FILLS CDZVZW (Z PART)
*
5     SR=SQRT(4.D0*R-1.D0)
      AT=ATAN(SR/(2.D0*R-1.D0))
      V1ZZ=-5.5D0-8.D0*(F1-SPENCE(2.D0))
      SPERR=SPENCE(1.D0+1.D0/R)
      V1ZW=-3.5D0-2.D0*R-(3.D0+2.D0*R)*ALR-2.D0*(1.D0+R)**2*(F1-SPERR)
      V2ZWW=2.D0/9.D0/R2+43.D0/18.D0/R-1.D0/6.D0-2.D0*R
     *     +(-1.D0/12.D0/R2-1.5D0/R+7.D0/3.D0+2.D0*R)*SR*AT
     *     -2.D0*R*(2.D0+R)*AT**2
*
      IF(INDF.EQ.5) THEN
*
       CALL VTBANA(1,AMZ2,WWv2,WWv11,WWv12)
       QBM=1D0/3D0
      VTB=V_TB**2*(R*WWv2-.5D0*(1D0-2D0*R1*(1D0-QBM))*WWv11-.5D0*WWv12)      
*
      ELSE
       VTB=0.D0
      ENDIF
      GO TO 9
*
* W-BOSON CHAIN *********************
* FILLS CDZVZW (W PART)
*
8     ALAM=AMZ2*AMZ2-4.D0*AMW2*AMZ2
      V1WZ=-5.D0-2.D0/R+(3.D0+2.D0/R)*ALR
     *    -2.D0*R1W2/R2*(SPENCE(1.D0)-SPENCE(R1W))
      V2WWZ=-9.D0/4.D0/R-1.D0/12.D0/R2+23.D0/18.D0
     *     +(1.D0/2.D0/R-3.D0/4.D0/R2
     *     -1.D0/24.D0/R/R2+1.D0)*ALR
     *     -DREAL(XL(-AMW2,AMW2,AMZ2))
     *     *(5.D0/6.D0/R+1.D0/24.D0/R2+1.D0/2.D0)/AMW2
     *     +(1.D0/2.D0+1.D0/R)*ALAM*DREAL(XJ(-AMW2,AMW2,AMZ2))
     *     *DREAL(XJ(-AMW2,AMW2,AMZ2))-(1.D0/2.D0+1.D0/R)*ALR*ALR
9     CONTINUE
*
      END

and in ZFITTER/dizet:



      SUBROUTINE VTBANA(NUNI,S,WWv2,WWv11,WWv12)   
*
* Supplies all ingredients for off-resonance EW finite m_t corrections
*
      IMPLICIT REAL*8(A-H,O-W,Y-Z)
      IMPLICIT COMPLEX*16(X)
*
      COMMON/CDZCON/PI,PI2,F1,D3,ALFAI,AL4PI,AL2PI,AL1PI
      COMMON/CDZWSM/AMW2,AMZ2,R,R1,R12,R2,AMH2,RW,RW1,RW12,RW2,RZ,RZ1,
     *      RZ12,RZ2,ALR,ALRW,ALRZ,SW2M,CW2M,AKSX,R1W,R1W2
      COMMON/CDZFER/CLM(8),AML(8),CQM(8),AMQ(8),VB,VT,VB2,VB2T,VT2,VT2T
*
      RWS =AMW2/S
      AMT2=AMQ(5)**2
      RTW =AMT2/AMW2
      RTW1=RTW-1D0
      ALRT=LOG(RTW)
*
      CALL S3WANA(AMT2,AMW2,-S,XJ0W,XS3W,XS3W0)
      CALL S3WANA(AMW2,AMT2,-S,XJ0T,XS3T,XS3T0)
*
      AJ0W=DREAL(XJ0W)
      AJ0T=DREAL(XJ0T)
      S3W =DREAL(XS3W)
      S3W0=DREAL(XS3W0)
      S3T =DREAL(XS3T)
      S3T0=DREAL(XS3T0)
*
      WWv2 =-2D0*RWS*(2D0+RWS)*S*(S3w-S3w0)
     &      +RTW*((3D0*RWS**2+2.5D0*RWS-2D0-(2D0*RWS-.5D0)*RTW
     &           +RWS*(.5D0-RWS)*RTW**2)*S*S3w
     &           -(RWS+1D0-(.5D0-RWS)*RTW)*(AJ0w-2D0)
     &           +(2D0*RWS+3D0/2/RTW1**2-2D0/RTW1+1D0/2
     &           -(.5D0-RWS)*RTW)*ALRT
     &           -(RWS+3D0/2/RTW1+3D0/4-(.5D0-RWS)*RTW)
     &           +.25D0/RWS*(AJ0w-3D0)*NUNI
     &           )
      WWv11=+2D0*(1D0+RWS)**2*S*(S3t-S3t0)
     &      +(2D0*RWS+3D0)*(AJ0t+ALRT+LOG(RWS))
     &      -RTW*(RWS*(3D0*RWS+2D0-RTW-RWS*RTW**2)*S*S3t
     &           +(RWS+.5D0+RWS*RTW)*(AJ0t+ALRT-2D0)
     &           -(2D0*RWS+3D0/2/RTW1**2-2D0/RTW1+1D0/2+RWS*RTW)*ALRT
     &           +RWS+3D0/2/RTW1+5D0/4+RWS*RTW
     &           ) 
      WWv12=-RTW*(RWS*(2D0+RWS-2D0*RWS*RTW+RWS*RTW**2)*S*S3t
     &           -(.5D0-RWS+RWS*RTW)*(AJ0t+ALRT-1D0)+RWS*RTW*ALRT
     &           )
*
      END

may be found in Gfitter/GSM/GSMMATH.cxx:



   // eq. hep-ph/9709229v1 (265)
   // see also in hep-ph/9908433 (A.4.33)
   m_V1ZW           = ( -3.5 - 2.0*R - (3.0 + 2.0*R)*TMath::Log(R) - 2.0*(1.0 + R)*(1.0 + R)
                        *(GMath::Zeta2() - TMath::DiLog(1.0 + 1.0/R)) + I*imag(V1b(-MZ2,MW2)) );
  
   // eq. hep-ph/9709229v1 (266)
   // see also in hep-ph/9908433 (A.4.34)
   m_V2ZWW          = ( 2.0/(9.0*R*R) + 43.0/(18.0*R) - 1.0/6.0 - 2.0*R
                        + (-1.0/(12.0*R*R) - 1.5/R + 7.0/3.0 + 2.0*R)*Sqr*Atan - 2.0*R*(2.0 + R)*Atan*Atan );  
  
   Double_t lam = GMath::IPow(MZ2,2) - 4.0*MW2*MZ2;
   
   // for W decay
   // see dizet6_42.f (ZFitter) line 3376-3480
  
   m_V1WZ  = ( -5.0 - 2.0/R + (3.0 + 2.0/R)*TMath::Log(R)
               -2.0*GMath::IPow((1.0+R)/R,2)*(GMath::Zeta2() - TMath::DiLog(1.0 + R)) ); 
   m_V2WWZ = ( -9/(4.0*R) -1/(12.0*R*R) + 23/18.0 
               + (0.5/R - 0.75/(R*R) - 1/(24.0*GMath::IPow(R,3)) + 1.0)*TMath::Log(R)
               - real(GSMMath::L(-MW2,MW2,MZ2))*(5/(6.0*R) + 1/(24.0*R*R) + 0.5)/MW2
               + (0.5 + 1.0/R)*lam*GMath::IPow( real(GSMMath::J(-MW2,MW2,MZ2)), 2 )
               - (0.5 + 1.0/R)*GMath::IPow( TMath::Log(R), 2 ) );

   // top quark additions
   Double_t RtW      = mt2/MW2;
   Double_t RtW1     = RtW - 1.0;
   
   Double_t J0W = 0, S3W = 0, S30W = 0;
   Double_t J0t = 0, S3t = 0, S30t = 0;

   // s = -MZ2
   GSMMath::S3Wana( mt2, MW2, -MZ2, J0W, S3W, S30W);
   GSMMath::S3Wana( MW2, mt2, -MZ2, J0t, S3t, S30t);
  
   // Information to this point in hep-ph/9709229 page 88-89,
   // hep-ph/9908433 page 175-177 
   // and dizet6_42.f (ZFitter) line 3376-3480
   Double_t WWv2  = ( - 2.0*R*(2.00 + R)*MZ2*(S3W - S30W) + RtW
                      *((3.0*R*R + 2.5*R - 2.0 - (2.0*R - 0.5)*RtW +R*(0.5 - R)*RtW*RtW)*MZ2*S3W
                        -(R + 1.00 - (0.5 - R)*RtW)*(J0W - 2.0) +(2.0*R + 3/(2.0*RtW1*RtW1) 
                                                                  - 2.0/RtW1 + 0.5 - (0.5 - R)*RtW)*TMath::Log(RtW)
                        -(R + 3/(2.0*RtW1) + 0.75 - (0.5 - R)*RtW) + 0.25/R*(J0W - 3.0)*1.0) );
   Double_t WWv11 = ( + 2.0*(1.0 + R)*(1.0 + R)*MZ2*(S3t-S30t) + (2.0*R + 3.0)*(J0t + TMath::Log(RtW) + TMath::Log(R))
                      - RtW*( R*(3.0*R + 2.0 - RtW - R*RtW*RtW)*MZ2*S3t + (R + 0.5 + R*RtW)*(J0t + TMath::Log(RtW) -
2.0)
                              - (2.00*R + 3/(2.0*RtW1*RtW1) - 2.0/RtW1 + 0.5 + R*RtW)*TMath::Log(RtW)
                              + R + 3/(2.0*RtW1) + 5/4.0 + R*RtW ) ); 
   Double_t WWv12 = ( -RtW*(R*(2.0 + R - 2.0*R*RtW + R*RtW*RtW)*MZ2*S3t
                            -(0.5 - R + R*RtW)*(J0t + TMath::Log(RtW) - 1.0) + R*RtW*TMath::Log(RtW) ) );

   Double_t v_tb  = 1;
  
   m_Vtb          = v_tb*v_tb*( R*WWv2 - 0.5*(1.0 - 2.0*(1.0 - R)*(2/3.0))*WWv11 - 0.5*WWv12 );
                                                   
   // now parameters are up-to-date
   SetUpToDate();
}




Further, 
in ZFITTER/dizet:



*
      XUFF=0.25D0/R*(1D0-6D0*CH*R1+12D0*R12*CH2)*XV1ZZ
     &    +(0.5D0-R-CH*R1)*XV1ZW+R*V2ZWW+VTB
*
      XRO1=AL4PI/R1*(DREAL(XZM1A+XZFM1A)-W0A+5.D0/8.D0*R*(1D0+R)
     &   -11.D0/2.D0-9.D0/4.D0*R/R1*ALR+2D0*XUFF)
*
      XAK1=AL4PI/R1*(R/R1*DREAL(XZM1A-XWM1A)
     &    +XAMM1A+R12/R*CH2*XV1ZZ-XUFF)



while in Gfitter/GSM/Z0ZFitter.cxx quite similar:



 * Class  : Z0ZFitter                                                             *
 *                                                                                *
 * Description:                                                                   *
 *      Auxiliary Theory of the ZFitter option using the OMS approach             *
 *      Computes effective weak mixing angle and Partial Z widths                 *
 *                                                                                *
 * Sources:                                                                       *
 *      hep-ph/9709229v1, hep-ph/9412201v3, hep-ph/9908433                        *
 *      Zfitter package dizet6_42.f                                               *
 *                                                                                *
 * Authors (alphabetical):                                                        *
 *      Martin Goebel     - DESY, Germany                  *
 *      Andreas Hoecker  - CERN, Switzerland              *
 *                                                                                *
 * Copyright (c) 2006:                                                            *
 *      CERN, Switzerland,                                                        *
 *





// eq. (255) of hep-ph/9709229v1
  case kCharm:
      uff = ( 0.25/m_R*(1.0 - 6.0*TMath::Abs(Charge)*(1.0-m_R) 
                        + 12.0*Charge*Charge*(1.0-m_R)*(1.0-m_R))*GetVertex().GetV1ZZ()
              + (0.5 - m_R - TMath::Abs(Charge)*(1.0-m_R))*GetVertex().GetV1ZW() 
              + m_R*GetVertex().GetV2ZWW() );

// leading order of rhof defined in (253) of hep-ph/9709229v1
   case kCharm:
      rho = ( GConstants::alphaQED()/(4*TMath::Pi()*(1.0-m_R))*
              ( real(m_ZAtMZ + m_ZFAtMZ) - m_WAt0 + 5.0/8.0*m_R*(1.0+m_R) 
                - 11.0/2.0 - 9.0*m_R/(4.0*(1.0-m_R))*TMath::Log(m_R) + 2.0*Uff(ParticleType,
Charge))

// leading order to kappaf defined in (254) of hep-ph/9709229v1
   case kCharm:
      kappa = ( GConstants::alphaQED()/(4*TMath::Pi()*(1-m_R))*
                ( m_R/(1-m_R)*real(m_ZAtMZ - m_WAtMW) 
                  + m_MPhoZAtMZ + GMath::IPow((1-m_R),2)/m_R*Charge*Charge*GetVertex().GetV1ZZ() 
                  - Uff(ParticleType, Charge) ) ); 



This looks quite similar, so one may assume that Gfitter also here did an `integration' from
ZFITTER.


At the other hand, in the reference given, hep-ph/9709229v1, the formulae look the same.
This might be a hint that the code in Gfitter is not `integrated' from ZFITTER but was typed in
following the publication hep-ph/9709229v1.


This is not easy to prove, because the corresponding parts of hep-ph/9709229v1 were `latexized'
one-to-one from ZFITTER wherever appropriate.


But let us have an additional look into two latex sources:


for Gfitter: EPJC60:smfit08/Appendix.tex, downloaded from arXive


for ZFITTER: EWWGR.tex, downloaded from arXive


We did this 3 March 2011, and discovered in EPJC60:smfit08/Appendix.tex as a comment line:
 %   bible II.A.6   [ {\sum}_{\sss{ZZ}}^{\prime{\rm Bos},F}(M_Z^2) \ ]

This is strange, because only we "Russians" used the keyword "bible" in our internal
communications. 


Furthermore, we found comments:
 % Real. A.5.       [ {V}_{1V}(s) ]
 % Real. A.6.       [  V_{{2W}}(s) ] 
% Realistic A.10.   [ \Pzg^{F}(\mzs) ]

All these comments may be found also in hep-ph/9709229v1:EWWGR.tex [in the part written by Bardin,
Kalinovskaya, Riemann, Riemann]:
%   bible II.A.6    [ Z^{^F}_b(M_Z^2) ]
% Realistic A.10.   [ M(s) ]
% Real. A.5.        [ {V}_{_{1V}}(s) ]
% Real. A.6.        [  V_{_{2W}}(s)  ]

Looking at the Latex lines, it becomes evident that dozens of lines are just copied from
ZFITTER/EWWGR.tex and adapted in Gfitter/Appendix.tex.


Other references given in addition are irrelevant.


Having this in mind, it becomes very probable that not only the latex lines were `integrated' [what
is evident] but also the [more sensitive] Fortran lines.


An interesting additional question arises immediately:
In Mr. Geoebel's diploma thesis, the corrsponding formulae look identical with those of EPC60, the
main Gfitter paper.

See for example:


(A.1) to (A.19) of diploma and (64) to (73) of EPJC60.


One has to be very naive to assume that though EPJC60 contains text copied-adapted from
ZFITTER/EWWWGR.tex, but Goebel's diploma text does not. If the authors want to disprove the
assumption, please deliver the original latex source of Mr. Goebel's diploma thesis.


The point is not that the diploma thesis reproduces formulae from ZFITTER, once they are quoted.
But, additionally, they are just copied from there, and this is, for a diploma thesis, unusual.
The minimum of openness would be that the author says: I use the formulae, and what I am writing
uses even the latex of the quoted reference.
 

To conclude this part: We did not give a systematic study of Fortran and Latex which was
`integrated ' from ZFITTER to Gfitter.
The interested researcher may look into the files and will discover dozens or hundreds of lines.
What may be taken for granted:


Not only Fortran, also Latex was taken as much as was considered needed.
And all this was not mentioned to ZFITTER or to the public. 



Compare also for "Vertex functions for W and Z decays" for details on Fortran `integrations' of
some vertex functions discussed here.

Additional examples are available.

Copyright © Tord Riemann, zfitter.com, 2011
Die Vervielfältigung, Verbreitung und Veröffentlichung unterliegt der Creative Commons-Lizenz [Namensnennung-Keine kommerzielle Nutzung-Keine Bearbeitung 3.0 Deutschland License, by-nc-nd]
Webmaster: Tord Riemann, zfitter.com
Created: 03. Aug 2011, last modified: 05. Aug 2011
Disclaimer

ZFITTER code `integration' in Gfitter software - a Documentation of basic facts -

Webpage under construction

Wo ZFITTER drin ist, soll auch ZFITTER draufstehen google translator: Where there is ZFITTER, should also stand upon ZFITTER

"Dieser Code wurde nicht fuer die Oeffentlichkeit gemacht, und das haben Sie zu respektieren."

Zero Tolerance to Plagiarism -- Null Toleranz fuer Plagiate

List of ZFITTER Fortran files and of Gfitter c++ classes involved

09 March 2011: First Proof of Evidence of `integrations'by 4 examples which were presented this date and during the days after to collegues, including some of the supporters of Gfitter --

Since 11 May 2011: Additional Evidence of `integrations' by examples presented to Gfitter representatives, supporters and `experts'

Wo ZFITTER drin ist, soll auch ZFITTER draufstehen

google translator:
Where there is ZFITTER, should also stand upon ZFITTER

09 March 2011:
First Proof of Evidence of `integrations'
by 4 examples which were presented this date and during the days after to collegues, including some of the supporters of Gfitter --

Since 11 May 2011:
Additional Evidence of `integrations'
by examples presented to Gfitter representatives, supporters and `experts'